fdm::FDMSecondCenteralDiff< Type > Struct Template Reference

finite difference method: second centeral diff More...

#include <FDMSecondCenteralDiff.hpp>

Inheritance diagram for fdm::FDMSecondCenteralDiff< Type >:

Collaboration diagram for fdm::FDMSecondCenteralDiff< Type >:

Public Member Functions
virtual void	updateAllCoef ()
	update all coefficients of FDM More...
auto &	updateCoefDW ()
	update the coefs of the first derivation at Rw More...
auto &	updateCoefDP ()
	update the coefs of the first derivation at Rp More...
auto &	updateCoefDDW ()
	update the coefs of the second derivation at Rw More...
auto &	updateCoefDDP ()
	update the coefs of the second derivation at Rp More...
auto &	updateCoefInterpW2P ()
	update the coefs of interpolation from Rw to Rp More...
auto &	updateCoefInterpP2W ()
	update the coefs of interpolation from Rp to Rw More...
auto &	updateCoefDW2P ()
	update the coefs of the first deriation from Rw to Rp More...
auto &	updateCoefDP2W ()
	update the coefs of the first deriation from Rp to Rw More...
auto &	updateCoefHelm ()
	update the coefs of helmholtz equation More...
auto &	updateStride (int sd_p, int sd_w)
	update the stride More...
auto &	updateStrideIn (int sd_p)
auto &	updateStrideOut (int sd_w)
template<typename T >
void	diffAtRw (T in[], T out[], Real alpha=1., Real beta=0.)
	Diff at Rw. More...
template<int Dir, typename T_Field >
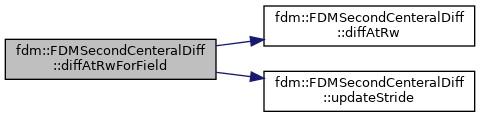
void	diffAtRwForField (T_Field &in, T_Field &out, Real alpha=1.0, Real beta=0.)
template<typename T >
void	diffAtRwxA (T in[], T xA[], T out[], Real alpha=1., Real beta=0.)
template<int Dir, typename T_Field >
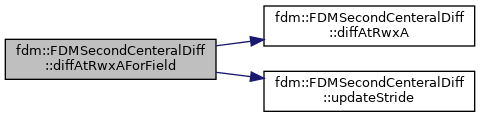
void	diffAtRwxAForField (T_Field &in, T_Field &xA, T_Field &out, Real alpha=1.0, Real beta=0.)
template<typename T >
void	diffAtRp (T in[], T out[], Real alpha=1., Real beta=0.)
	Diff at Rp. More...
template<int Dir, typename T_Field >
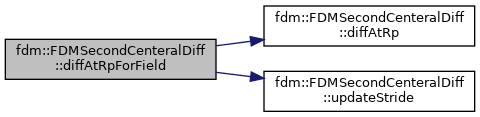
void	diffAtRpForField (T_Field &in, T_Field &out, Real alpha=1.0, Real beta=0.)
template<typename T >
void	diffAtRpxA (T in[], T xA[], T out[], Real alpha=1., Real beta=0.)
template<int Dir, typename T_Field >
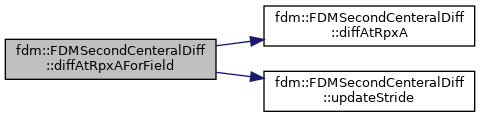
void	diffAtRpxAForField (T_Field &in, T_Field &xA, T_Field &out, Real alpha=1.0, Real beta=0.)
template<typename T >
void	diff2AtRw (T in[], T out[], Real alpha=1., Real beta=0.)
	second Diff at Rw More...
template<int Dir, typename T_Field >
void	diff2AtRwForField (T_Field &in, T_Field &out, Real alpha=1.0, Real beta=0.)
template<typename T >
void	diff2AtRp (T in[], T out[], Real alpha=1., Real beta=0.)
	Second Diff at Rp. More...
template<int Dir, typename T_Field >
void	diff2AtRpForField (T_Field &in, T_Field &out, Real alpha=1.0, Real beta=0.)
template<typename T >
void	interpFromRwToRp (T in[], T out[], Real alpha=1., Real beta=0.)
template<int Dir, typename T_Field >
void	interpFromRwToRpForField (T_Field &in, T_Field &out, Real alpha=1.0, Real beta=0.)
template<typename T >
void	interpFromRwToRpxA (T in[], T xA[], T out[], Real alpha=1., Real beta=0.)
template<int Dir, typename T_Field >
void	interpFromRwToRpxAForField (T_Field &in, T_Field &xA, T_Field &out, Real alpha=1.0, Real beta=0.)
template<typename T >
void	interpFromRpToRw (T in[], T out[], Real alpha=1., Real beta=0.)
template<int Dir, typename T_Field >
void	interpFromRpToRwForField (T_Field &in, T_Field &out, Real alpha=1.0, Real beta=0.)
template<typename T >
void	interpFromRpToRwxA (T in[], T xA[], T out[], Real alpha=1., Real beta=0.)
template<int Dir, typename T_Field >
void	interpFromRpToRwxAForField (T_Field &in, T_Field &xA, T_Field &out, Real alpha=1.0, Real beta=0.)
template<typename T >
void	diffFromRpToRw (T in[], T out[], Real alpha=1., Real beta=0.)
template<int Dir, typename T_Field >
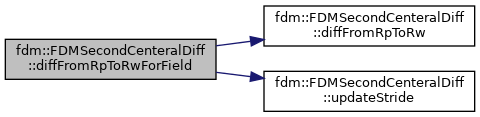
void	diffFromRpToRwForField (T_Field &in, T_Field &out, Real alpha=1.0, Real beta=0.)
template<typename T >
void	diffFromRwToRp (T in[], T out[], Real alpha=1., Real beta=0.)
template<int Dir, typename T_Field >
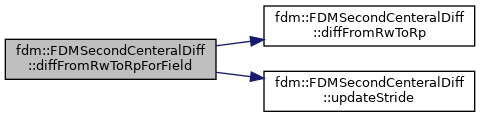
void	diffFromRwToRpForField (T_Field &in, T_Field &out, Real alpha=1.0, Real beta=0.)
template<typename T0 , typename T1 >
void	solveHelmholtzAtRp (T0 lam[], T1 rhs[], T1 out[], const blockelm::BoundaryType btype0=blockelm::BoundaryType::Neumann, const T0 bval0=0., const blockelm::BoundaryType btype1=blockelm::BoundaryType::Neumann, const T0 bval1=0.)
	Solve helmholtz equation f''+lam f=rhs. More...
template<typename T0 , typename T1 >
void	solveHelmholtzAtRw (T0 lam[], T1 rhs[], T1 out[], const blockelm::BoundaryType btype0=blockelm::BoundaryType::Neumann, const T0 bval0=0., const blockelm::BoundaryType btype1=blockelm::BoundaryType::Neumann, const T0 bval1=0.)
template<typename T0 , typename T1 >
void	explicitBoundaryAtRp (T0 in[], const blockelm::BoundaryType btype0=blockelm::BoundaryType::Neumann, const T1 bval0=0., const blockelm::BoundaryType btype1=blockelm::BoundaryType::Neumann, const T1 bval1=0.)
template<int Dir, typename T_Field , typename T1 >
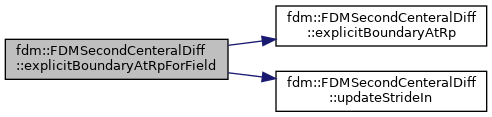
void	explicitBoundaryAtRpForField (T_Field &in, const blockelm::BoundaryType btype0=blockelm::BoundaryType::Neumann, const T1 bval0=0., const blockelm::BoundaryType btype1=blockelm::BoundaryType::Neumann, const T1 bval1=0.)
template<int Dir, typename T_Field >
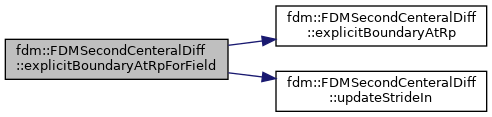
void	explicitBoundaryAtRpForField (T_Field &in, auto &boundary0, auto &boundary1)
template<typename T0 , typename T1 >
void	explicitBoundaryAtRw (T0 in[], const blockelm::BoundaryType btype0=blockelm::BoundaryType::Neumann, const T1 bval0=0., const blockelm::BoundaryType btype1=blockelm::BoundaryType::Neumann, const T1 bval1=0.)
template<int Dir, typename T_Field , typename T1 >
void	explicitBoundaryAtRwForField (T_Field &in, const blockelm::BoundaryType btype0=blockelm::BoundaryType::Neumann, const T1 bval0=0., const blockelm::BoundaryType btype1=blockelm::BoundaryType::Neumann, const T1 bval1=0.)
template<int Dir, typename T_Field >
void	explicitBoundaryAtRwForField (T_Field &in, auto &boundary0, auto &boundary1)
Public Member Functions inherited from fdm::FDMDiffBase
auto &	setMesh (const int num, const Real R[], FDMWPTag tag)
auto &	setMeshFromRw (const int num, const Real R[])
auto &	updateGhostMesh (int ghost)

Additional Inherited Members
Public Attributes inherited from fdm::FDMDiffBase
int	nm
int	gh = 1
blin::Array2r	coef_dw
blin::Array2r	coef_dp
blin::Array2r	coef_dw2p
blin::Array2r	coef_dp2w
blin::Array2r	coef_ddw
blin::Array2r	coef_ddp
blin::Array2r	coef_interp_w2p
blin::Array2r	coef_interp_p2w
blin::Array2r	coef_ddw2p
blin::Array2r	coef_ddp2w
blin::Array1r	xw
blin::Array1r	xp
blin::Array1r	helm_u
blin::Array1r	helm_l
int	dist
int	stride_in = 1
int	stride_out = 1

Detailed Description

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>
struct fdm::FDMSecondCenteralDiff< Type >

finite difference method: second centeral diff

Template Parameters

Type

Member Function Documentation

diff2AtRp()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T >

void fdm::FDMSecondCenteralDiff< Type >::diff2AtRp ( T  in[], T  out[], Real  alpha = 1., Real  beta = 0.  )

inline

Second Diff at Rp.

Template Parameters

T

Parameters

in
out
alpha
beta

References fdm::FDMDiffBase::coef_ddp, fdm::FDMDiffBase::gh, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::stride_out.

Here is the caller graph for this function:

diff2AtRpForField()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::diff2AtRpForField ( T_Field &  in, T_Field &  out, Real  alpha = 1.0, Real  beta = 0.  )

inline

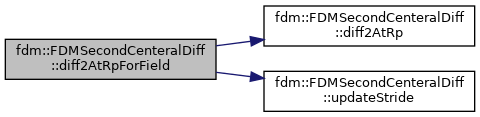
References fdm::FDMSecondCenteralDiff< Type >::diff2AtRp(), and fdm::FDMSecondCenteralDiff< Type >::updateStride().

Here is the call graph for this function:

diff2AtRw()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T >

void fdm::FDMSecondCenteralDiff< Type >::diff2AtRw ( T  in[], T  out[], Real  alpha = 1., Real  beta = 0.  )

inline

second Diff at Rw

Template Parameters

T

Parameters

in
out
alpha
beta

References fdm::FDMDiffBase::coef_ddw, fdm::FDMDiffBase::gh, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::stride_out.

Here is the caller graph for this function:

diff2AtRwForField()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::diff2AtRwForField ( T_Field &  in, T_Field &  out, Real  alpha = 1.0, Real  beta = 0.  )

inline

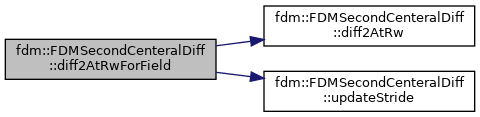
References fdm::FDMSecondCenteralDiff< Type >::diff2AtRw(), and fdm::FDMSecondCenteralDiff< Type >::updateStride().

Here is the call graph for this function:

diffAtRp()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T >

void fdm::FDMSecondCenteralDiff< Type >::diffAtRp ( T  in[], T  out[], Real  alpha = 1., Real  beta = 0.  )

inline

Diff at Rp.

Template Parameters

T

Parameters

in
out
alpha
beta

References fdm::FDMDiffBase::coef_dp, fdm::FDMDiffBase::gh, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::stride_out.

Here is the caller graph for this function:

diffAtRpForField()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::diffAtRpForField ( T_Field &  in, T_Field &  out, Real  alpha = 1.0, Real  beta = 0.  )

inline

References fdm::FDMSecondCenteralDiff< Type >::diffAtRp(), and fdm::FDMSecondCenteralDiff< Type >::updateStride().

Here is the call graph for this function:

diffAtRpxA()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T >

void fdm::FDMSecondCenteralDiff< Type >::diffAtRpxA ( T  in[], T  xA[], T  out[], Real  alpha = 1., Real  beta = 0.  )

inline

References fdm::FDMDiffBase::coef_dp, fdm::FDMDiffBase::gh, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::stride_out.

Here is the caller graph for this function:

diffAtRpxAForField()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::diffAtRpxAForField ( T_Field &  in, T_Field &  xA, T_Field &  out, Real  alpha = 1.0, Real  beta = 0.  )

inline

References fdm::FDMSecondCenteralDiff< Type >::diffAtRpxA(), and fdm::FDMSecondCenteralDiff< Type >::updateStride().

Here is the call graph for this function:

diffAtRw()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T >

void fdm::FDMSecondCenteralDiff< Type >::diffAtRw ( T  in[], T  out[], Real  alpha = 1., Real  beta = 0.  )

inline

Diff at Rw.

Template Parameters

T

Parameters

in
out
alpha
beta

References fdm::FDMDiffBase::coef_dw, fdm::FDMDiffBase::gh, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::stride_out.

Here is the caller graph for this function:

diffAtRwForField()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::diffAtRwForField ( T_Field &  in, T_Field &  out, Real  alpha = 1.0, Real  beta = 0.  )

inline

References fdm::FDMSecondCenteralDiff< Type >::diffAtRw(), and fdm::FDMSecondCenteralDiff< Type >::updateStride().

Here is the call graph for this function:

diffAtRwxA()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T >

void fdm::FDMSecondCenteralDiff< Type >::diffAtRwxA ( T  in[], T  xA[], T  out[], Real  alpha = 1., Real  beta = 0.  )

inline

References fdm::FDMDiffBase::coef_dw, fdm::FDMDiffBase::gh, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::stride_out.

Here is the caller graph for this function:

diffAtRwxAForField()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::diffAtRwxAForField ( T_Field &  in, T_Field &  xA, T_Field &  out, Real  alpha = 1.0, Real  beta = 0.  )

inline

References fdm::FDMSecondCenteralDiff< Type >::diffAtRwxA(), and fdm::FDMSecondCenteralDiff< Type >::updateStride().

Here is the call graph for this function:

diffFromRpToRw()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T >

void fdm::FDMSecondCenteralDiff< Type >::diffFromRpToRw ( T  in[], T  out[], Real  alpha = 1., Real  beta = 0.  )

inline

References fdm::FDMDiffBase::coef_dp2w, fdm::FDMDiffBase::gh, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::stride_out.

Here is the caller graph for this function:

diffFromRpToRwForField()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::diffFromRpToRwForField ( T_Field &  in, T_Field &  out, Real  alpha = 1.0, Real  beta = 0.  )

inline

References fdm::FDMSecondCenteralDiff< Type >::diffFromRpToRw(), and fdm::FDMSecondCenteralDiff< Type >::updateStride().

Here is the call graph for this function:

diffFromRwToRp()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T >

void fdm::FDMSecondCenteralDiff< Type >::diffFromRwToRp ( T  in[], T  out[], Real  alpha = 1., Real  beta = 0.  )

inline

References fdm::FDMDiffBase::coef_dw2p, fdm::FDMDiffBase::gh, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::stride_out.

Here is the caller graph for this function:

diffFromRwToRpForField()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::diffFromRwToRpForField ( T_Field &  in, T_Field &  out, Real  alpha = 1.0, Real  beta = 0.  )

inline

References fdm::FDMSecondCenteralDiff< Type >::diffFromRwToRp(), and fdm::FDMSecondCenteralDiff< Type >::updateStride().

Here is the call graph for this function:

explicitBoundaryAtRp()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T0 , typename T1 >

void fdm::FDMSecondCenteralDiff< Type >::explicitBoundaryAtRp ( T0  in[], const blockelm::BoundaryType  btype0 = blockelm::BoundaryType::Neumann, const T1  bval0 = 0., const blockelm::BoundaryType  btype1 = blockelm::BoundaryType::Neumann, const T1  bval1 = 0.  )

inline

References blockelm::Dirichlet, fdm::FDMDiffBase::gh, blockelm::LR, blockelm::Neumann, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::xp.

Here is the caller graph for this function:

explicitBoundaryAtRpForField() [1/2]

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::explicitBoundaryAtRpForField ( T_Field &  in, auto &  boundary0, auto &  boundary1  )

inline

References fdm::FDMSecondCenteralDiff< Type >::explicitBoundaryAtRp(), and fdm::FDMSecondCenteralDiff< Type >::updateStrideIn().

Here is the call graph for this function:

explicitBoundaryAtRpForField() [2/2]

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field , typename T1 >

void fdm::FDMSecondCenteralDiff< Type >::explicitBoundaryAtRpForField ( T_Field &  in, const blockelm::BoundaryType  btype0 = blockelm::BoundaryType::Neumann, const T1  bval0 = 0., const blockelm::BoundaryType  btype1 = blockelm::BoundaryType::Neumann, const T1  bval1 = 0.  )

inline

References fdm::FDMSecondCenteralDiff< Type >::explicitBoundaryAtRp(), and fdm::FDMSecondCenteralDiff< Type >::updateStrideIn().

Here is the call graph for this function:

explicitBoundaryAtRw()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T0 , typename T1 >

void fdm::FDMSecondCenteralDiff< Type >::explicitBoundaryAtRw ( T0  in[], const blockelm::BoundaryType  btype0 = blockelm::BoundaryType::Neumann, const T1  bval0 = 0., const blockelm::BoundaryType  btype1 = blockelm::BoundaryType::Neumann, const T1  bval1 = 0.  )

inline

References blockelm::Dirichlet, fdm::FDMDiffBase::gh, blockelm::LR, blockelm::Neumann, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::xw.

Here is the caller graph for this function:

explicitBoundaryAtRwForField() [1/2]

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::explicitBoundaryAtRwForField ( T_Field &  in, auto &  boundary0, auto &  boundary1  )

inline

References fdm::FDMSecondCenteralDiff< Type >::explicitBoundaryAtRw(), and fdm::FDMSecondCenteralDiff< Type >::updateStrideIn().

Here is the call graph for this function:

explicitBoundaryAtRwForField() [2/2]

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field , typename T1 >

void fdm::FDMSecondCenteralDiff< Type >::explicitBoundaryAtRwForField ( T_Field &  in, const blockelm::BoundaryType  btype0 = blockelm::BoundaryType::Neumann, const T1  bval0 = 0., const blockelm::BoundaryType  btype1 = blockelm::BoundaryType::Neumann, const T1  bval1 = 0.  )

inline

References fdm::FDMSecondCenteralDiff< Type >::explicitBoundaryAtRw(), and fdm::FDMSecondCenteralDiff< Type >::updateStrideIn().

Here is the call graph for this function:

interpFromRpToRw()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T >

void fdm::FDMSecondCenteralDiff< Type >::interpFromRpToRw ( T  in[], T  out[], Real  alpha = 1., Real  beta = 0.  )

inline

References fdm::FDMDiffBase::coef_interp_p2w, fdm::FDMDiffBase::gh, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::stride_out.

Here is the caller graph for this function:

interpFromRpToRwForField()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::interpFromRpToRwForField ( T_Field &  in, T_Field &  out, Real  alpha = 1.0, Real  beta = 0.  )

inline

References fdm::FDMSecondCenteralDiff< Type >::interpFromRpToRw(), and fdm::FDMSecondCenteralDiff< Type >::updateStride().

Here is the call graph for this function:

interpFromRpToRwxA()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T >

void fdm::FDMSecondCenteralDiff< Type >::interpFromRpToRwxA ( T  in[], T  xA[], T  out[], Real  alpha = 1., Real  beta = 0.  )

inline

References fdm::FDMDiffBase::coef_interp_p2w, fdm::FDMDiffBase::gh, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::stride_out.

Here is the caller graph for this function:

interpFromRpToRwxAForField()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::interpFromRpToRwxAForField ( T_Field &  in, T_Field &  xA, T_Field &  out, Real  alpha = 1.0, Real  beta = 0.  )

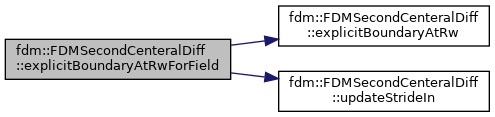
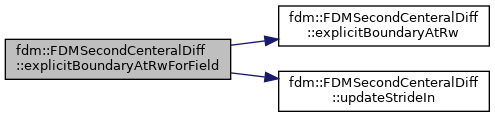
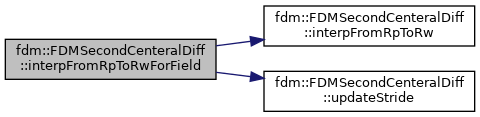
inline

References fdm::FDMSecondCenteralDiff< Type >::interpFromRpToRwxA(), and fdm::FDMSecondCenteralDiff< Type >::updateStride().

Here is the call graph for this function:

interpFromRwToRp()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T >

void fdm::FDMSecondCenteralDiff< Type >::interpFromRwToRp ( T  in[], T  out[], Real  alpha = 1., Real  beta = 0.  )

inline

References fdm::FDMDiffBase::coef_interp_w2p, fdm::FDMDiffBase::gh, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::stride_out.

Here is the caller graph for this function:

interpFromRwToRpForField()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::interpFromRwToRpForField ( T_Field &  in, T_Field &  out, Real  alpha = 1.0, Real  beta = 0.  )

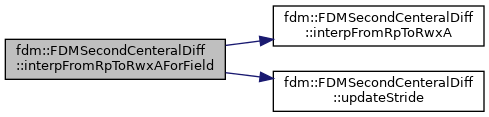
inline

References fdm::FDMSecondCenteralDiff< Type >::interpFromRwToRp(), and fdm::FDMSecondCenteralDiff< Type >::updateStride().

Here is the call graph for this function:

interpFromRwToRpxA()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T >

void fdm::FDMSecondCenteralDiff< Type >::interpFromRwToRpxA ( T  in[], T  xA[], T  out[], Real  alpha = 1., Real  beta = 0.  )

inline

References fdm::FDMDiffBase::coef_interp_w2p, fdm::FDMDiffBase::gh, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::stride_out.

Here is the caller graph for this function:

interpFromRwToRpxAForField()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<int Dir, typename T_Field >

void fdm::FDMSecondCenteralDiff< Type >::interpFromRwToRpxAForField ( T_Field &  in, T_Field &  xA, T_Field &  out, Real  alpha = 1.0, Real  beta = 0.  )

inline

References fdm::FDMSecondCenteralDiff< Type >::interpFromRwToRpxA(), and fdm::FDMSecondCenteralDiff< Type >::updateStride().

Here is the call graph for this function:

solveHelmholtzAtRp()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T0 , typename T1 >

void fdm::FDMSecondCenteralDiff< Type >::solveHelmholtzAtRp ( T0  lam[], T1  rhs[], T1  out[], const blockelm::BoundaryType  btype0 = blockelm::BoundaryType::Neumann, const T0  bval0 = 0., const blockelm::BoundaryType  btype1 = blockelm::BoundaryType::Neumann, const T0  bval1 = 0.  )

inline

Solve helmholtz equation f''+lam f=rhs.

Template Parameters

T
T1

Parameters

lam
rhs
out	f
btype0	boundary type for lower boundary
bval0	boundary value for lower boundary
btype1	boundary type for upper boundary
bval1	boudnary value for upper boundary

Returns

auto&

References fdm::FDMDiffBase::coef_ddp, blockelm::Dirichlet, fdm::FDMSecondCenteralDiff< Type >::explicitBoundaryAtRp(), fdm::FDMDiffBase::gh, fdm::FDMDiffBase::helm_l, fdm::FDMDiffBase::helm_u, blockelm::Neumann, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, fdm::FDMDiffBase::stride_out, and fdm::FDMDiffBase::xp.

Here is the call graph for this function:

Here is the caller graph for this function:

solveHelmholtzAtRw()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

template<typename T0 , typename T1 >

void fdm::FDMSecondCenteralDiff< Type >::solveHelmholtzAtRw ( T0  lam[], T1  rhs[], T1  out[], const blockelm::BoundaryType  btype0 = blockelm::BoundaryType::Neumann, const T0  bval0 = 0., const blockelm::BoundaryType  btype1 = blockelm::BoundaryType::Neumann, const T0  bval1 = 0.  )

inline

References fdm::FDMDiffBase::coef_ddw, blockelm::Dirichlet, fdm::FDMSecondCenteralDiff< Type >::explicitBoundaryAtRw(), fdm::FDMDiffBase::gh, fdm::FDMDiffBase::helm_l, fdm::FDMDiffBase::helm_u, blockelm::Neumann, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::stride_in, fdm::FDMDiffBase::stride_out, and fdm::FDMDiffBase::xw.

Here is the call graph for this function:

Here is the caller graph for this function:

updateAllCoef()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

virtual void fdm::FDMSecondCenteralDiff< Type >::updateAllCoef ( )

inlinevirtual

update all coefficients of FDM

Implements fdm::FDMDiffBase.

References fdm::FDMSecondCenteralDiff< Type >::updateCoefDW().

Here is the call graph for this function:

updateCoefDDP()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

auto& fdm::FDMSecondCenteralDiff< Type >::updateCoefDDP ( )

inline

update the coefs of the second derivation at Rp

Returns

auto&

References fdm::FDMDiffBase::coef_ddp, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::xp, and fdm::FDMDiffBase::xw.

updateCoefDDW()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

auto& fdm::FDMSecondCenteralDiff< Type >::updateCoefDDW ( )

inline

update the coefs of the second derivation at Rw

Returns

auto&

References fdm::FDMDiffBase::coef_ddw, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::xp, and fdm::FDMDiffBase::xw.

updateCoefDP()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

auto& fdm::FDMSecondCenteralDiff< Type >::updateCoefDP ( )

inline

update the coefs of the first derivation at Rp

Returns

auto&

References fdm::FDMDiffBase::coef_dp, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::xp, and fdm::FDMDiffBase::xw.

updateCoefDP2W()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

auto& fdm::FDMSecondCenteralDiff< Type >::updateCoefDP2W ( )

inline

update the coefs of the first deriation from Rp to Rw

Returns

auto&

References fdm::FDMDiffBase::coef_dp2w, fdm::FDMDiffBase::nm, and fdm::FDMDiffBase::xp.

updateCoefDW()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

auto& fdm::FDMSecondCenteralDiff< Type >::updateCoefDW ( )

inline

update the coefs of the first derivation at Rw

Returns

auto&

References fdm::FDMDiffBase::coef_dw, fdm::FDMDiffBase::nm, and fdm::FDMDiffBase::xp.

Here is the caller graph for this function:

updateCoefDW2P()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

auto& fdm::FDMSecondCenteralDiff< Type >::updateCoefDW2P ( )

inline

update the coefs of the first deriation from Rw to Rp

Returns

auto&

References fdm::FDMDiffBase::coef_dw2p, fdm::FDMDiffBase::nm, and fdm::FDMDiffBase::xw.

updateCoefHelm()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

auto& fdm::FDMSecondCenteralDiff< Type >::updateCoefHelm ( )

inline

update the coefs of helmholtz equation

f''+kf=g

Returns

auto&

References fdm::FDMDiffBase::helm_l, fdm::FDMDiffBase::helm_u, and fdm::FDMDiffBase::nm.

updateCoefInterpP2W()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

auto& fdm::FDMSecondCenteralDiff< Type >::updateCoefInterpP2W ( )

inline

update the coefs of interpolation from Rp to Rw

Returns

auto&

References fdm::FDMDiffBase::coef_interp_p2w, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::xp, and fdm::FDMDiffBase::xw.

updateCoefInterpW2P()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

auto& fdm::FDMSecondCenteralDiff< Type >::updateCoefInterpW2P ( )

inline

update the coefs of interpolation from Rw to Rp

Returns

auto&

References fdm::FDMDiffBase::coef_interp_w2p, fdm::FDMDiffBase::nm, fdm::FDMDiffBase::xp, and fdm::FDMDiffBase::xw.

updateStride()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

auto& fdm::FDMSecondCenteralDiff< Type >::updateStride ( int  sd_p, int  sd_w  )

inline

update the stride

Parameters

sd_p	stride for variable at Rp
sd_w	stride for variable at Rw

Returns

auto&

References fdm::FDMDiffBase::stride_in, and fdm::FDMDiffBase::stride_out.

Here is the caller graph for this function:

updateStrideIn()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

auto& fdm::FDMSecondCenteralDiff< Type >::updateStrideIn ( int  sd_p )

inline

References fdm::FDMDiffBase::stride_in.

Here is the caller graph for this function:

updateStrideOut()

template<FDMTAG_Type Type = FDMTAG_Type::Stretch>

auto& fdm::FDMSecondCenteralDiff< Type >::updateStrideOut ( int  sd_w )

inline

References fdm::FDMDiffBase::stride_out.

---

The documentation for this struct was generated from the following file:

• /mnt/e/linuxOS/PhyStar/FDM/DiffOp/FDMSecondCenteralDiff.hpp